Models with a single predictor

Lecture 16

Dr. Mine Çetinkaya-Rundel

Duke University
STA 199 - Fall 2022

10/25/22

Warm up

While you wait for class to begin…

Clone your ae-13 project from GitHub, render your document, update your name, and commit and push.

Announcements

  • My office hours on Zoom today (2-4pm): bit.ly/minezoom
  • Advising / info session on Zoom 1-2pm today. Will send link along with OH info as Sakai announcement.

Goals

  • Modeling with a single predictor
  • Model parameters, estimates, and error terms
  • Interpreting slopes and intercepts

Setup

library(tidyverse)
library(tidymodels)
library(fivethirtyeight) # for the fandango dataset

Models with a single predictor

Spurious correlations

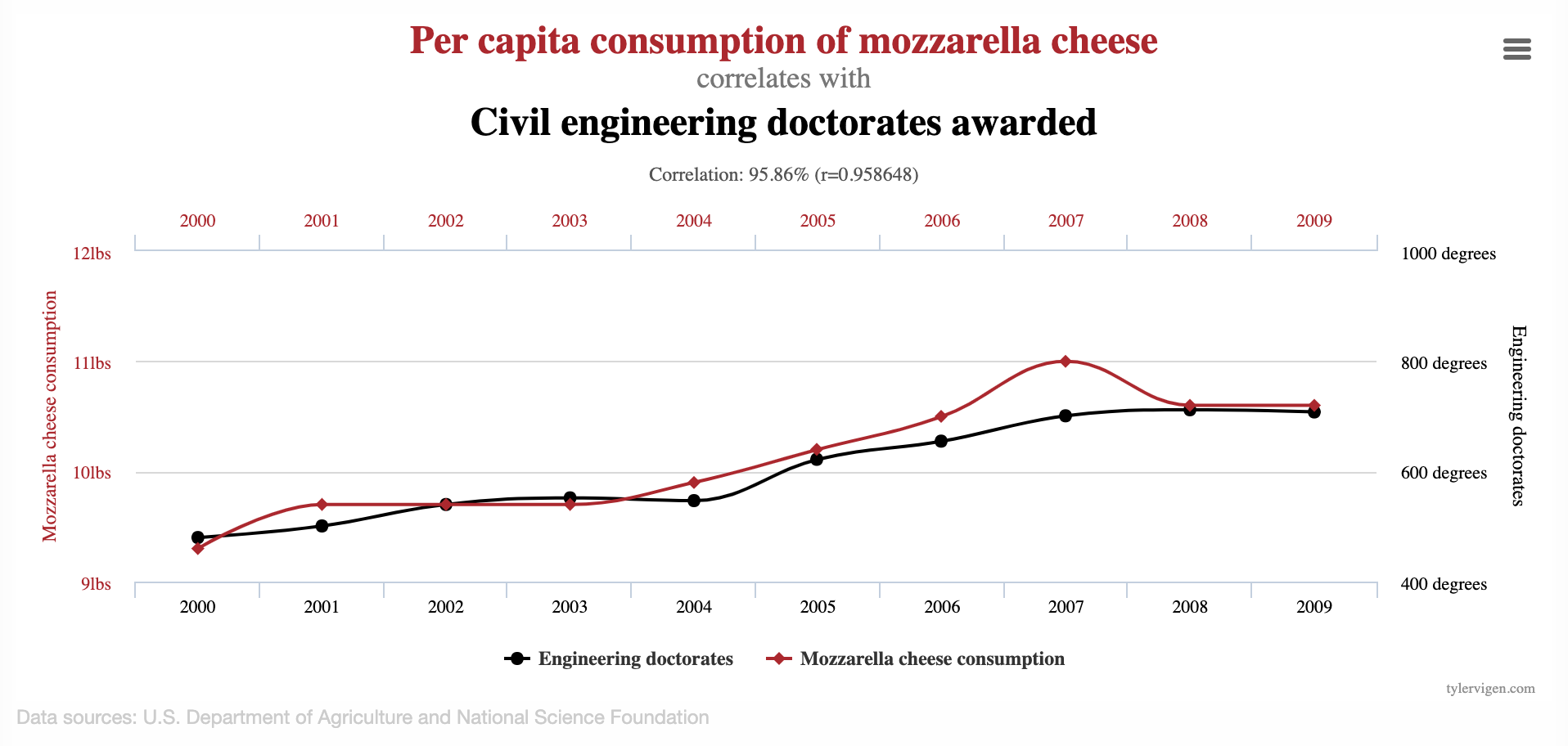
Spurious correlations

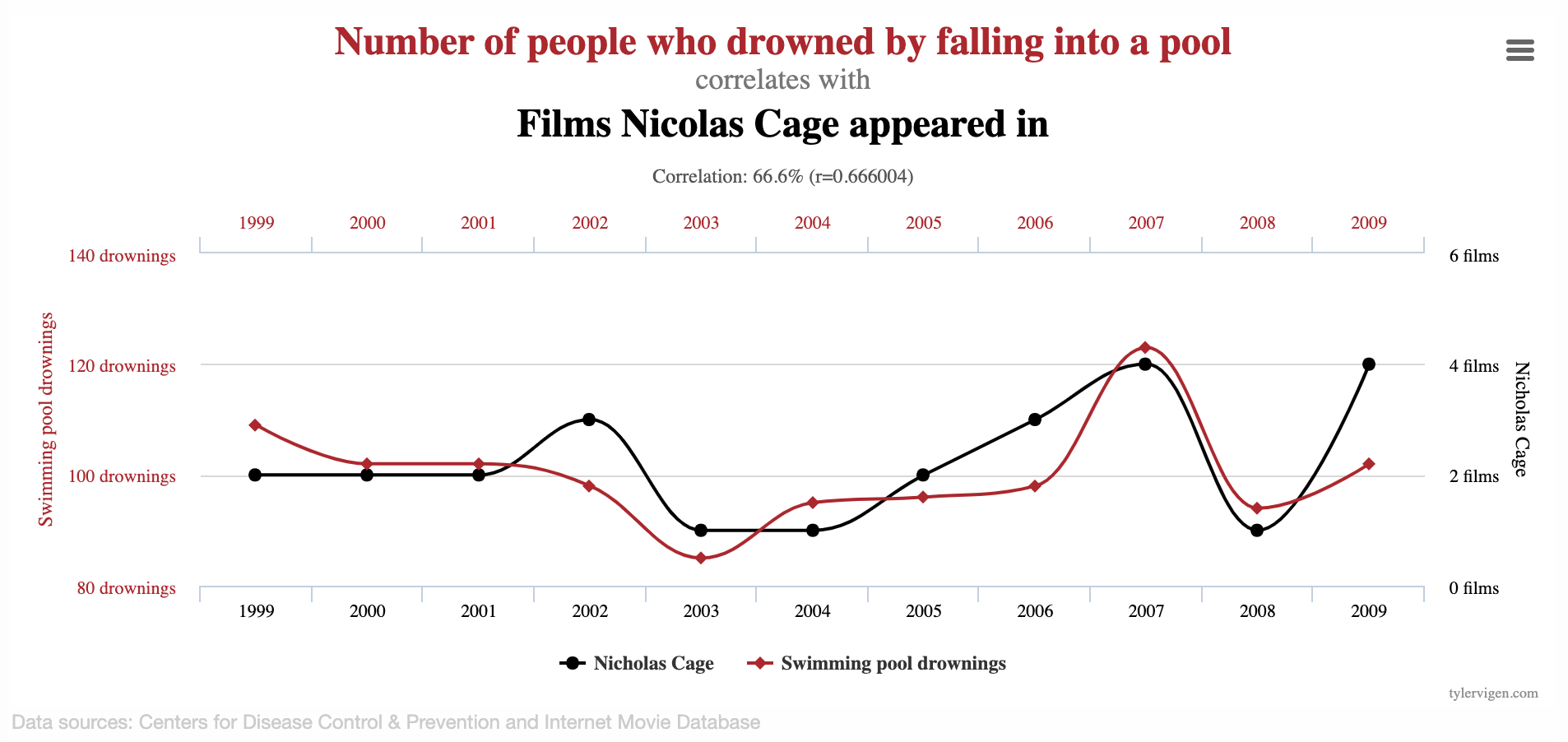
Linear regression with a single predictor

Data prep

  • Rename Rotten Tomatoes columns as critics and audience
  • Rename the dataset as movie_scores
movie_scores <- fandango %>%
  rename(
    critics = rottentomatoes, 
    audience = rottentomatoes_user
  )

Data overview

movie_scores |>
  select(critics, audience)
# A tibble: 146 × 2
   critics audience
     <int>    <int>
 1      74       86
 2      85       80
 3      80       90
 4      18       84
 5      14       28
 6      63       62
 7      42       53
 8      86       64
 9      99       82
10      89       87
# … with 136 more rows

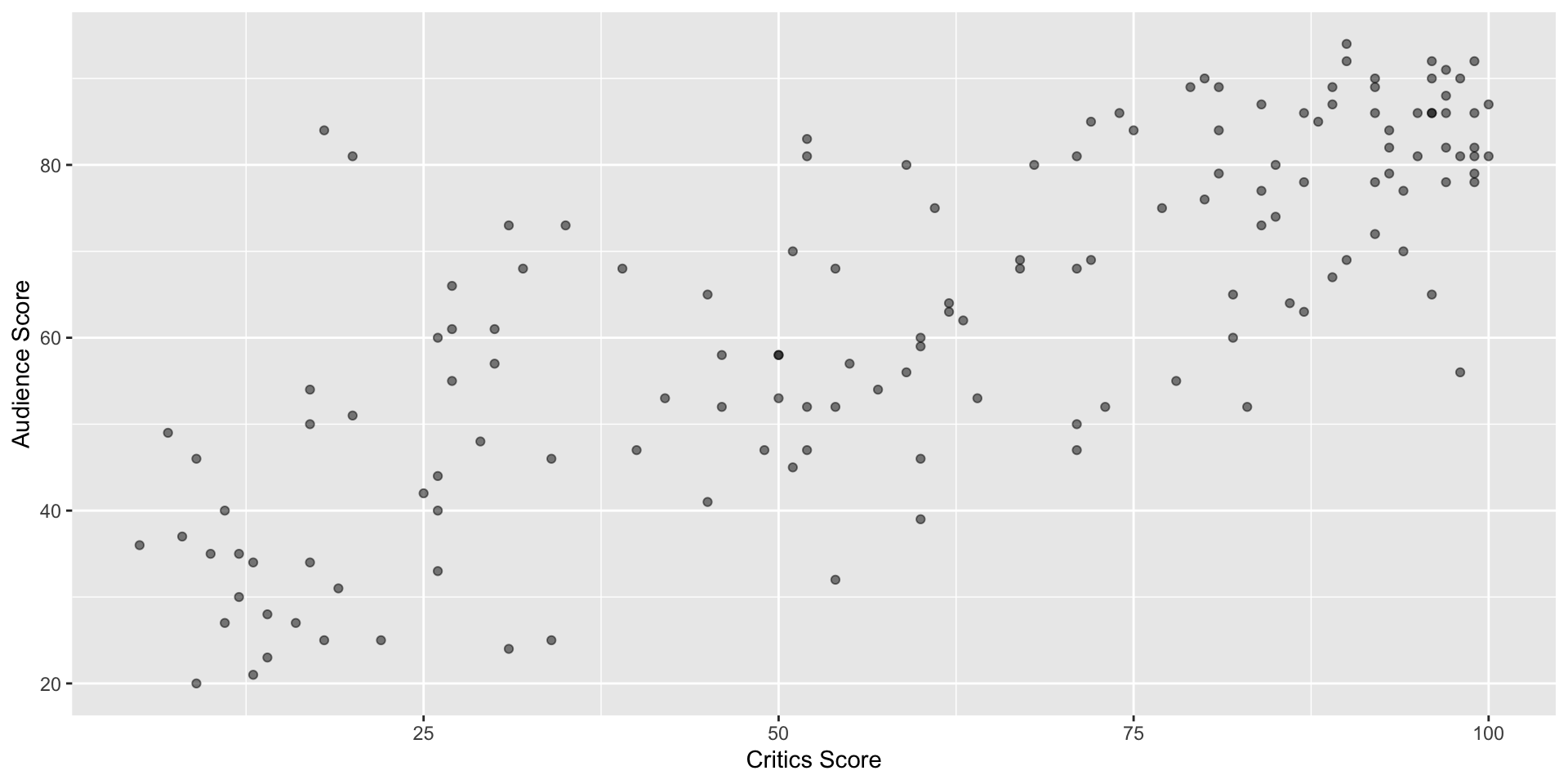
Data visualization

Regression model

A regression model is a function that describes the relationship between the outcome, \(Y\), and the predictor, \(X\).

\[\begin{aligned} Y &= \color{black}{\textbf{Model}} + \text{Error} \\[8pt] &= \color{black}{\mathbf{f(X)}} + \epsilon \\[8pt] &= \color{black}{\boldsymbol{\mu_{Y|X}}} + \epsilon \end{aligned}\]

Regression model

\[ \begin{aligned} Y &= \color{#325b74}{\textbf{Model}} + \text{Error} \\[8pt] &= \color{#325b74}{\mathbf{f(X)}} + \epsilon \\[8pt] &= \color{#325b74}{\boldsymbol{\mu_{Y|X}}} + \epsilon \end{aligned} \]

Simple linear regression

Use simple linear regression to model the relationthip between a quantitative outcome (\(Y\)) and a single quantitative predictor (\(X\)): \[\Large{Y = \beta_0 + \beta_1 X + \epsilon}\]

  • \(\beta_1\): True slope of the relationship between \(X\) and \(Y\)
  • \(\beta_0\): True intercept of the relationship between \(X\) and \(Y\)
  • \(\epsilon\): Error (residual)

Simple linear regression

\[\Large{\hat{Y} = b_0 + b_1 X}\]

  • \(b_1\): Estimated slope of the relationship between \(X\) and \(Y\)
  • \(b_0\): Estimated intercept of the relationship between \(X\) and \(Y\)
  • No error term!
  • These \(b_1\) and \(b_0\)

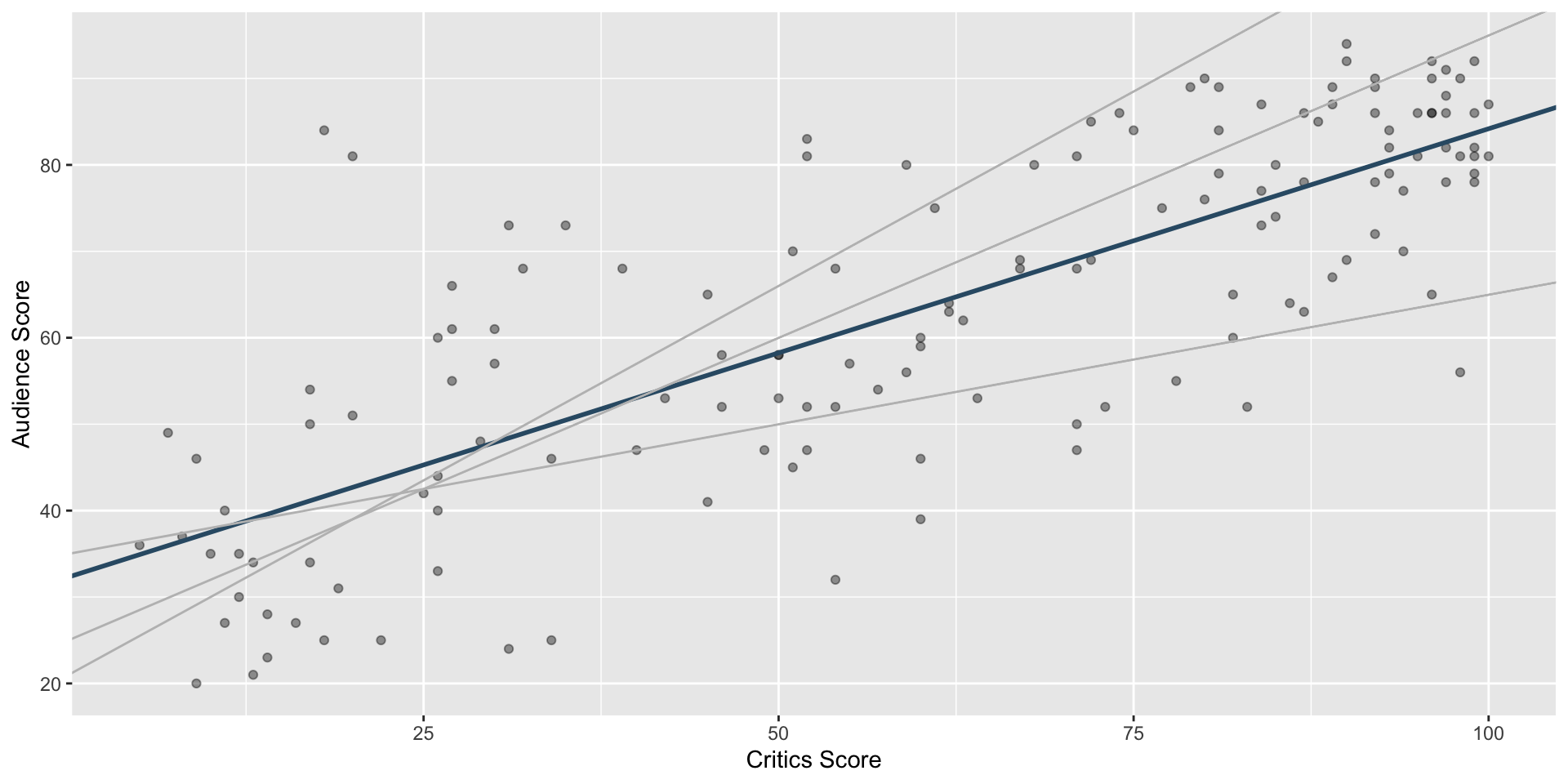
Choosing values for \(b_1\) and \(b_0\)

Residuals

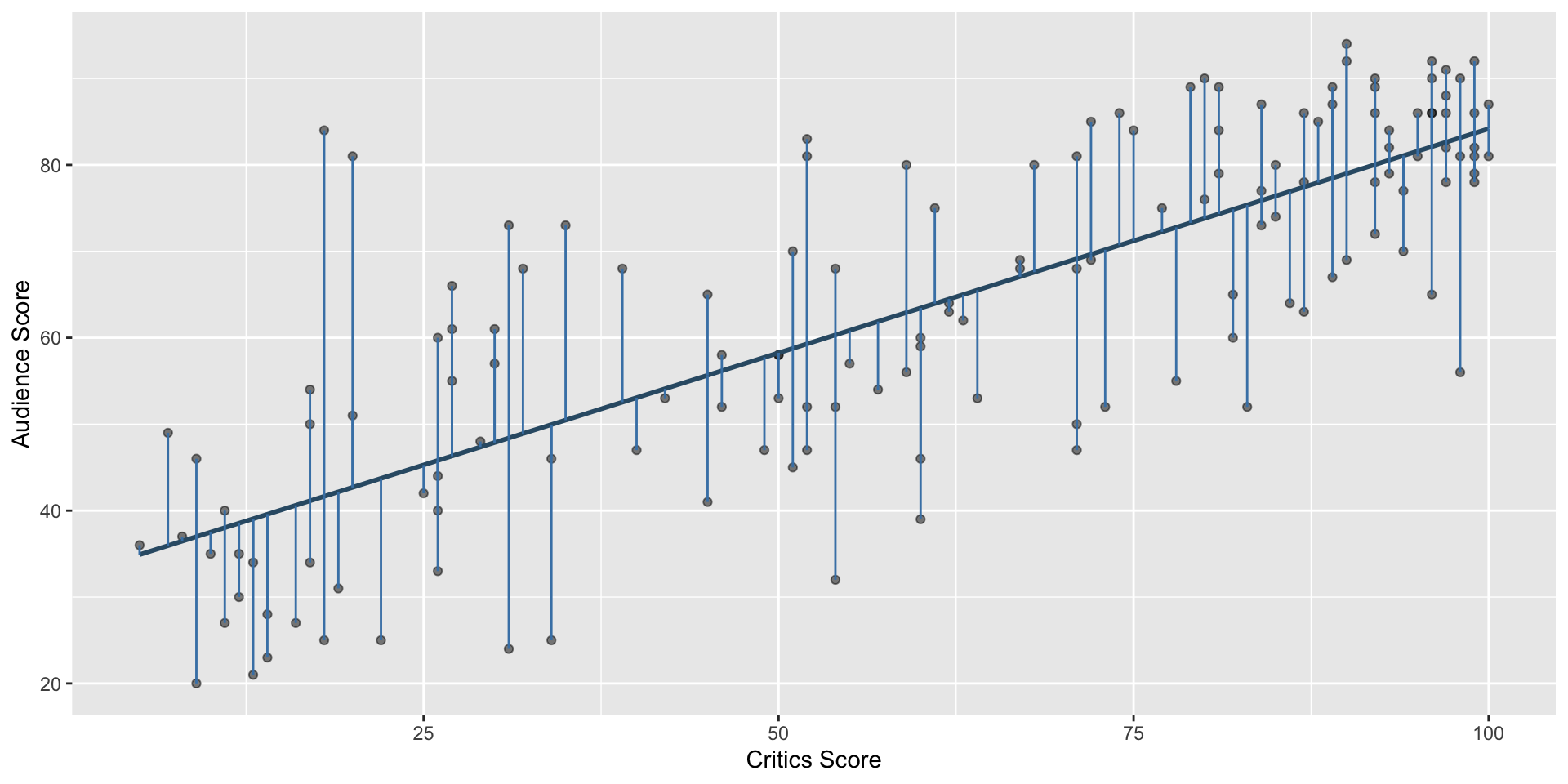
\[\text{residual} = \text{observed} - \text{predicted} = y - \hat{y}\]

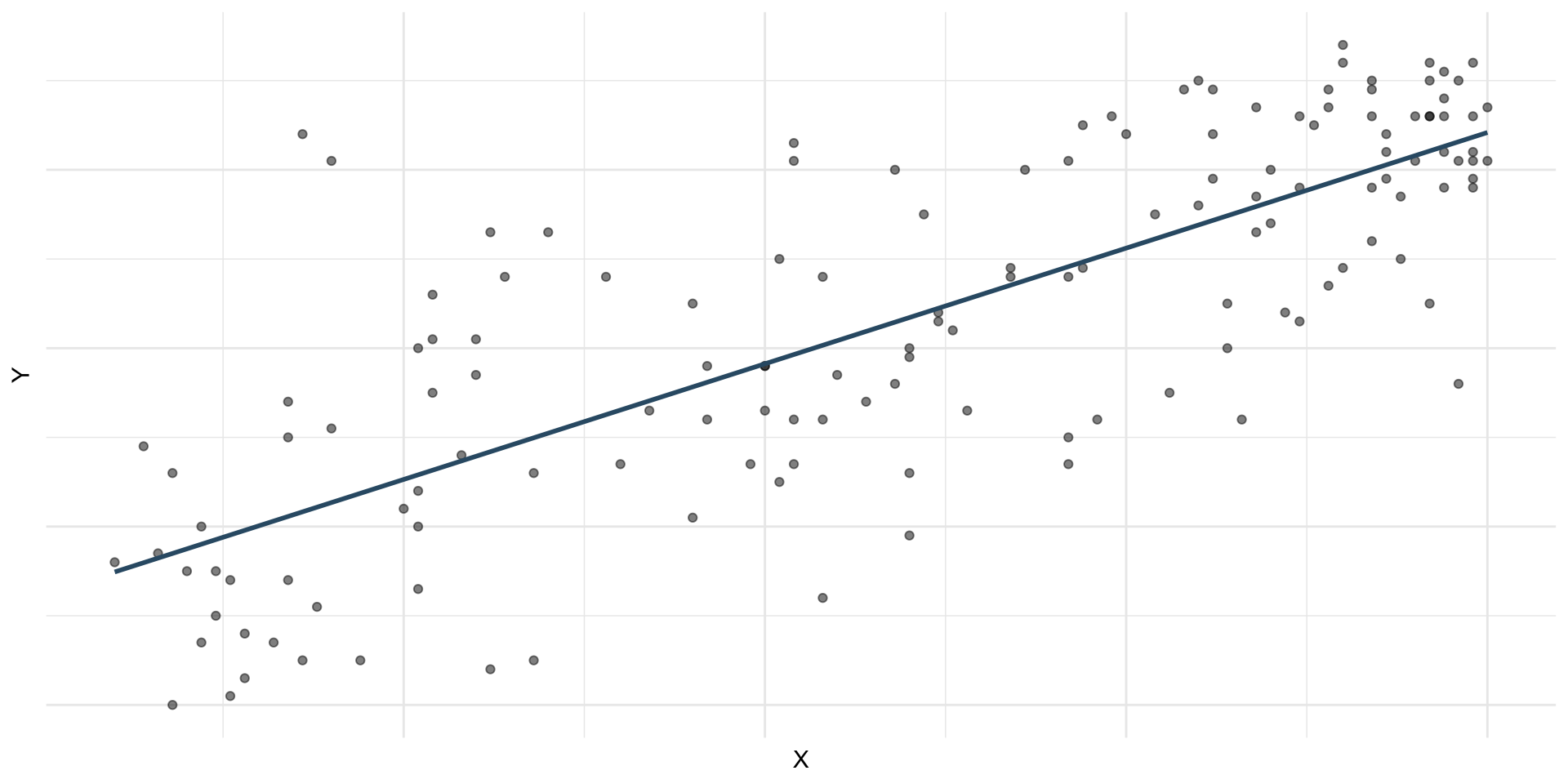
Least squares line

  • The residual for the \(i^{th}\) observation is

\[e_i = \text{observed} - \text{predicted} = y_i - \hat{y}_i\]

  • The sum of squared residuals is

\[e^2_1 + e^2_2 + \dots + e^2_n\]

  • The least squares line is the one that minimizes the sum of squared residuals

Least squares line

movies_fit <- linear_reg() |>
  fit(audience ~ critics, data = movie_scores)

tidy(movies_fit)
# A tibble: 2 × 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)   32.3      2.34        13.8 4.03e-28
2 critics        0.519    0.0345      15.0 2.70e-31

Slope and intercept

Properties of least squares regression

  • The regression line goes through the center of mass point (the coordinates corresponding to average \(X\) and average \(Y\)): \(b_0 = \bar{Y} - b_1~\bar{X}\)

  • Slope has the same sign as the correlation coefficient: \(b_1 = r \frac{s_Y}{s_X}\)

  • Sum of the residuals is zero: \(\sum_{i = 1}^n \epsilon_i = 0\)

  • Residuals and \(X\) values are uncorrelated

Interpreting the slope

slido.com / #sta199

Poll: The slope of the model for predicting audience score from critics score is 0.519. Which of the following is the best interpretation of this value?

  1. For every one point increase in the critics score, the audience score goes up by 0.519 points, on average.
  2. For every one point increase in the critics score, we expect the audience score to be higher by 0.519 points, on average.
  3. For every one point increase in the critics score, the audience score goes up by 0.519 points.
  4. For every one point increase in the audience score, the critics score goes up by 0.519 points, on average.

Interpreting slope & intercept

\[\widehat{\text{audience}} = 32.3 + 0.519 \times \text{critics}\]

  • Slope: For every one point increase in the critics score, we expect the audience score to be higher by 0.519 points, on average.
  • Intercept: If the critics score is 0 points, we expect the audience score to be 32.3 points.

Is the intercept meaningful?

✅ The intercept is meaningful in context of the data if

  • the predictor can feasibly take values equal to or near zero or
  • the predictor has values near zero in the observed data

🛑 Otherwise, it might not be meaningful!

Application exercise

ae-13

  • Go to the course GitHub org and find your ae-13 (repo name will be suffixed with your GitHub name).
  • Clone the repo in your container, open the Quarto document in the repo, and follow along and complete the exercises.
  • Render, commit, and push your edits by the AE deadline – 3 days from today.

🔗 sta199-f22-1.github.io